Cette vidéo🔥 correspond au webinaire en différé organisé pour la publication de l’article : Etude des Déterminants sur la Variabilité du Coût d’Assurance Maladie. A travers cette vidéo, vous découvrirez une nouvelle méthode, notamment l’utilisation des algorithmes de Machine Learning⚡ dans le domaine d’Assurance. Mais également, elle revient sur les compétences requises pour réaliser une telle approche.
Tables des Matières :
Introduction
Analyse Exploratoire des Données (EDA)
Aspect Théorique des Modèles d’Apprentissage Automatique : cas d’une Régression Linéaire
Application : Prédiction du Coût d’Assurance Maladie
Analyse des Facteurs sur le Coût de la Couverture d’Assurance Maladie
Conclusion
1. Introduction
La plupart des facteurs qui influent sur le montant que nous payons pour l’assurance maladie échappent à notre contrôle. Néanmoins, il serait plus utile d’avoir une meilleure compréhension de ce qu’ils sont réellement. A cet effet, la modélisation constitue l’une des meilleures solutions dans l’estimation des montants d’assurance. Et de nos jours, avec l’avènement de la science des données ou data science en anglais, on parvient à mieux évaluer les facteurs de risque à partir des données historiques.
La Data Science : définition
La Data Science est un domaine interdisciplinaire qui utilise des méthodes statistiques, informatiques et mathématiques pour extraire des connaissances et des informations à partir de données. Il implique la collecte, le nettoyage, la préparation, l’analyse, la modélisation et la visualisation des données pour répondre à des questions et résoudre des problèmes dans divers domaines tels que les affaires, la santé, la science, la technologie et la finance, entre autres. Les professionnels de la Data Science utilisent des outils tels que les langages de programmation (Python, R, etc.), les bases de données, les techniques de fouille de données, l’apprentissage automatique et l’intelligence artificielle pour extraire des connaissances exploitables à partir des données. Les applications courantes de la Data Science incluent l’analyse de marché, la recommandation de produits, la détection de fraude, la prédiction de la demande, l’optimisation des opérations et la prévision de tendances. La Data Science joue un rôle de plus en plus important dans l’économie moderne et est considérée comme l’une des compétences les plus demandées sur le marché du travail.
La Data Science dans la prédiction des primes d’assurance
La Data Science a longtemps été utilisée pour la prédiction des primes d’assurance en utilisant des modèles prédictifs basés sur l’analyse de données historiques et des facteurs de risque. Les données historiques peuvent inclure des informations sur les réclamations précédentes, les types de véhicules, les antécédents de conduite et d’autres facteurs pertinents. Les modèles prédictifs peuvent utiliser des techniques statistiques telles que la régression linéaire, la régression logistique, les arbres de décision et les réseaux de neurones pour prédire les primes d’assurance. Les données peuvent également être analysées en utilisant des techniques de fouille de données et d’apprentissage automatique pour identifier des modèles et des tendances qui peuvent aider à prédire les risques et les coûts futurs associés à l’assurance. Les résultats de ces analyses peuvent être utilisés par les compagnies d’assurance pour ajuster leurs primes en fonction des risques identifiés et pour améliorer leur rentabilité et leur précision en matière de tarification.
Machine Learning pour extraire des connaissances exploitables à partir des données
Etant donné l’un des fondamentaux sur lequel repose la Data Science, le Machine Learning constitue la possibilité à donner à la machine la capacité à apprendre sans pour autant qu’elle soit explicitement programmée pour ça. Noter que dans le domaine des assurances, il peut être utilisé pour la prédiction des primes en utilisant des algorithmes d’apprentissage supervisé tels que la régression linéaire, la régression logistique, les forêts aléatoires, les réseaux de neurones, etc. Ces algorithmes peuvent être entraînés à partir de données historiques sur les réclamations précédentes, les types de véhicules, les antécédents de conduite et d’autres facteurs pertinents, afin de prédire la prime d’assurance pour un nouvel ensemble de données. Les algorithmes d’apprentissage automatique peuvent également être utilisés pour découvrir des tendances et des relations cachées entre les différents facteurs qui affectent le coût des réclamations, ce qui peut aider les compagnies d’assurance à ajuster leurs tarifs en conséquence et à améliorer leur rentabilité. Cependant, il est important de noter que l’utilisation du Machine Learning pour la tarification de l’assurance soulève également des questions d’éthique et de transparence, et que les compagnies d’assurance doivent prendre en compte ces facteurs lors de la mise en place de ces modèles de tarification.
2. Analyse Exploratoire des Données (EDA)
Données et variables utilisées dans cette étude :
La base utilisée dans cet article constitue des données personnelles sur les coûts de l’assurance médicale. Elles proviennent du site Kaggle (lien du dataset) et concernent 1338 individus observés suivant 7 variables à savoir :
| Variables | Catégorie de Variable | Signification |
|---|---|---|
| age | continue | Age du bénéficiaire |
| sex | qualitative | Sexe du bénéficiaire |
| bmi | continue | Indice de Massse Corporelle du bénéficiaire |
| children | discrète | Nombre d’enfants du bénéficiaire |
| smoker | qualitative | Le bénéficiaire est t-il fumeur ? |
| region | qualitative | Zone de résidence du bénéficiaire |
| charges | continue | Coût de la couverture d’assurance |
Aperçu des Données
Dans la suite, nous procéderons à l’analyse univariée des données.
2.1 Analyse Univariée
Cas des Variables Continues :
Distribution des âges
L’histogramme ci-dessous montrent une forte présence de jeunes de moins de 20 ans dans nos données ainsi que de même pour ce qui est des bénéficiaires âgés entre 45 et 50 ans.
Entre autres, les données montrent que l’âge des bénéficiaires varie entre 18 et 64 ans et que ces derniers sont âgés en moyenne de 39 ans (voir Tab1).
| Variable | min | q25 | q50 (mediane) | moyenne | q75 | max |
|---|---|---|---|---|---|---|
| Âge | 18 | 27 | 39 | 39.02 | 51 | 64 |
Distribution de l’Indice de Massse Corporelle (IMC)
Apriori, l’histogramme ci-dessous semble déceler une tendance symétrique, pour ce qui de l’indice de masse corporelle (IMC). De plus, les données montrent que la plupart des IMC sont compris entre 25 et 30.
Par ailleurs, les données montrent que les indices de masse corporelle varient au environ de 16 à 53 au maximum. Et que ces derniers, en moyenne tournent au tour de 30 (voir Tab2).
| Variable | min | q25 | q50 (mediane) | moyenne | q75 | max |
|---|---|---|---|---|---|---|
| IMC | 15.96 | 26.29 | 30.4 | 30.66 | 34.69 | 53.13 |
Distribution des Charges (Coûts) d’Assurance
Apriori, l’histogramme ci-dessous semble déceler une tendance asymétrique (dissymétrie positive) avec une queue à droite, pour ce qui des coûts d’assurance. De plus, les données montrent que la majorité des charges n’excèdent pas 15 000 $.
Par ailleurs dans cet échantillon, si l’on prend l’une des moitiés des individus, alors les données montrent que la charge de leur couverture d’assurance atteint au moins ou au plus 9 382 $ (voir Tab3).
| Variable | min | q25 | q50 (mediane) | moyenne | q75 | max |
|---|---|---|---|---|---|---|
| Charges ($) | 1 121.87 | 4 740.28 | 9 382 | 13 270.42 | 16 639.91 | 63 770.43 |
Cas des Variables Qualitatives :
Répartition des Sexes
Les données montrent que dans cet échantillon, il y’a pratiquement autant d’hommes que de femmes (50.5% contre 49.5% voir la Fig4)
Répartition de la Taille des familles
Apriori, les données montrent que dans cet échantillon, on a pratiquement que des familles réduites, c’est-à-dire qui ont au plus 3 enfants et contrairement aux familles larges à plus de 3 enfants (97% contre 3% voir Fig5).
Répartition des Zones de Résidences
Contrairement aux autres zones des USA (sud-ouest, nord-est et le sud- ouest), le sud-est constitue la zone de résidence la plus fréquente de notre échantillon (27% contre 24% pour les zones sud-ouest, nord-est et le sud-ouest respectivement) (voir Fig6)
En effet, les États du sud, se caractérisent par une ouverture sur le golfe du Mexique, un climat tropical (sud de la Floride) et surtout subtropical, marqué par la chaleur et le passage des cyclones en été. La population possède des origines très diverses : les Afro-Américains sont relativement nombreux dans les anciens États esclavagistes, les Hispaniques sont particulièrement présents en Floride.
Dans la suite, nous procéderons à l’analyse bivariée des données.
2.2 Analyse Bivariée
Dans cette section, nous procéderons à une étude de dépendance, où il s’agira d’étudier la liaison entre le coût de la couverture d’assurance maladie et les autres variables comme : l’âge, le sexe, l’IMC etc…
L’idée sera de dire oui ou non, si la variation des charges d’assurance est liée à l’âge ou le sexe des bénéficiaires par exemple.
Cas des Variables Continues :
A priori, nous chercherons à étudier les liaisons entre les variables continues.
Corrélation des variables continues
D’après la matrice de corrélation ci-dessous (Fig7), on voit que malgré leur faiblesse, toutefois, tous les coefficients de corrélation restent positifs. Ainsi, les données montrent que l’âge et les charges d’assurance sont les deux variables les plus corrélées (corr = 0.29). Par conséquent, cela signifie que les charges les plus élevées sont observées chez les bénéficiaires les plus âgés. Entre autres, les données révèlent également les charges sont positivement liées (corr = 0.19) à l’indice de masse corporelle (IMC). Autrement, cela montre que les couvertures d’assurance les plus couteuses sont souvent notées chez les bénéficiaires dont l’IMC est plus élevé.
Distribution de la Charge d’Assurance (Coûts) selon l’Âge des bénéficiaires
Dans un premier temps, nous avons procédé à la catégorisation des âges en classes.
Ainsi, les données montrent une forte présence de jeunes de la vingtaine contrairement aux individus de la soixantaine qui sont peu présents dans cet échantillon (31% contre 9% voir Fig8).
Entre autres, les données révèlent que le coût de la couverture d’assurance maladie est d’autant plus élevé lorsqu’on se rapproche de la soixantaine d’année ou plus (voir Fig9).
En plus, comme l’association est statistiquement significative (p-value = 1.121e-13 < 0.05 = 5%), donc nous pouvons affirmer avec une haute certitude que la variabilité des charges de couverture d’assurance maladie est liée à l’âge des bénéficiaires.
Distribution de la Charge d’Assurance (Coûts) selon l’Indice de Masse Corporelle (IMC)
Comme le cas précédent, nous allons procéder dans un premier temps à la catégorisation de l’IMC en classes.
Ainsi, les données montrent une forte présence d’individus touchés par l’obésité dans cet échantillon (soit 53% de l’échantillon voir Fig10). Il s’agit d’un phénomène très récurrent aux USA.
Par ailleurs, les données révèlent que le coût de la couverture d’assurance maladie est d’autant plus élevé lorsqu’on se rapproche de l’obésité (IMC >= 30) (voir Fig11).
De plus, étant donné que l’association est statistiquement significative (p-value = 1.759e-13 < 0.05 = 5%), ainsi nous pouvons affirmer avec une haute certitude que la variabilité des charges de couverture d’assurance maladie est liée à l’indice de masse corporelle des bénéficiaires.
Cas des Variables Qualitatives :
Dans cette section, il s’agira d’étudier les liaisons entre les variables qualitatives par rapport à notre variable cible (Target) qui correspond ici au coût d’assurance (charges).
Distribution des charges d’assurance selon le sexe
En comparant le coût (médian) de la couverture d’assurance entre les sexes, on voit qu’il n’y a pratiquement pas de différence entre les hommes et les femmes. Par contre, si on prend les valeurs moyennes, alors les données montrent que les charges sont plus importantes chez hommes que chez les femmes (13 956.75 $ contre 12 569.58 $). De plus, les données révèlent que cette différence est statistiquement significative au risque de 5% (p-value = 0.03 < 0.05 = 5%). Ainsi nous pouvons affirmer avec une haute certitude que la variabilité des charges de couverture d’assurance maladie est liée au sexe des bénéficiaires.
Distribution des charges d’assurance selon les Régions
Pour ce qui est des régions (localités), les données montrent que les charges de couverture d’assurance sont plus élevées dans les zones-est et particulièrement du sud-est et du nord-est.
Distribution du Coût d’Assurance selon que l’on soit Fumeur
Selon que l’on s’intéresse aux fumeurs, les données révèlent que le coût (médian) de la couverture d’assurance est pratiquement 3 fois plus élevé chez les fumeurs que les non-fumeurs (34 456.35 $ contre 11 363.01 $). De plus, les données montrent que cette différence est statistiquement significative au risque de 5% (p-value < 2.2e-16). Ainsi nous pouvons affirmer avec une haute certitude que la variabilité des charges de couverture d’assurance maladie est liée au fait que le bénéficiaire soit ou pas un fumeur.
Variation du Coût d’Assurance en fonction de l’Âge et selon que l’on soit Fumeur
Là, il s’agit d’une analyse tridimensionnelle entre les charges, l’âge et le fait de fumer.
L’analyse bivariée à travers la Fig8 avait laissé entendre que les charges de couverture d’assurance étaient plus élevées chez les personnes les plus âgées. Toutefois, les données révèlent que les charges de couverture élevées concernent en réalité et le plus souvent les personnes qui fument du tabac (voir Fig15).
Variation du Coût d’Assurance en fonction de l’IMC et selon que l’on soit Fumeur
Comme le cas précédent, l’analyse bivariée à travers la Fig11 avait montré que les charges de couverture d’assurance étaient plus élevées chez les personnes dont l’IMC (indice de masse corporelle) était supérieur à 30 (présentent une obésité). Cependant, les données révèlent que les charges sont d’autant plus élevées chez les personnes qui fument que par rapport aux autres (voir Fig16).
3. Aspect Théorique des Modèles d’Apprentissage Automatique : cas d’une Régression Linéaire
La régression linéaire est le modèle par excellence pour comprendre le fonctionnement des algorithmes de Machine Learning.
3.1 La Régression Linéaire Simple :
En effet, il s’agit en réalité d’un algorithme d’apprentissage supervisé très basique qui vise à trouver la meilleure droite possible à l’aide d’une seule variable explicative (on parle aussi d’un seul degré de liberté). Entre autres, du fait de cette unique variable explicative, on parle de modèle univarié, par opposition aux modèles multivariés, qui font appel à plusieurs variables. Par ailleurs, leur simplicité permet d’introduire des notions qui peuvent devenir complexes lorsque l’on se place dans le cadre général. Ainsi, nous introduirons notamment la construction de la fonction de coût, qui mesure l’erreur que l’on fait en approximant nos données. Nous verrons que trouver les meilleurs paramètres de notre modèle équivaut à minimiser cette fonction de coût. Enfin, nous introduirons une méthode de résolution numérique dont l’intuition se trouve déjà dans les travaux du très vénérable Isaac Newton : la descente de gradient.
Cette section va donc expliciter les trois étapes nécessaires pour passer des données brutes au meilleur modèle de régression linéaire univarié. Ces étapes concernent :
la définition d’une fonction hypothèse ;
puis la construction d’une fonction de coût ;
et enfin la minimisation de cette fonction de coût.
Définition : Fonction Convexe :
Une fonction définie sur un intervalle réel 𝐼 est convexe lorsque pour tout \(x\) et \(y\) de \(I\) et tout \(t\) dans \([0, 1]\) on a :
\[ 𝑓(𝑡𝑥 + (1 − 𝑡 )𝑦) ≤ 𝑡𝑓(𝑥) + (1 − 𝑡 )𝑓(𝑦). \]
Définition de la fonction hypothèse :
Dans le cas de la régression linéaire univariée, on prend une hypothèse simplificatrice très forte : le modèle dépend d’une unique variable explicative, nommée \(X\). Cette variable est un entrant de notre problème, une donnée que nous connaissons. Par exemple, le nombre de pièces d’un appartement, une pression atmosphérique, le revenu de vos clients, ou n’importe quelle grandeur qui vous paraît influencer une cible, qu’on nommera \(Y\) et qui, pour continuer nos exemples, serait respectivement, le prix d’un appartement, le nombre de millilitres de pluie tombés, ou encore le montant du panier moyen d’achat de vos clients.
On cherche alors à trouver la meilleure fonction hypothèse, qu’on nommera \(h\) et qui aura pour rôle d’approximer les valeurs de sortie \(Y\) :
\[ h : X \longrightarrow Y \]
Dans le cas de la régression linéaire à une variable, la fonction hypothèse \(h\) sera de la forme :
\[ h(X) = \theta_{0} + \theta_{1}X \]
En représentation matricielle, \(\theta_{0}\) et \(\theta_{1}\) forment un vecteur \(\Theta\) tel que :
\[ \Theta = \left( \begin{array}{c} \theta_{0} \\ \theta_{1} \end{array} \right) \]
Ainsi, notre problème revient donc à trouver le meilleur couple \((\theta_{0}, \theta_{1})\) tel que \(h(x)\) soit « proche » de \(Y\) pour les couples \((x, y)\) de notre base de données.
Définition de la fonction coût :
La notion d’approximation induit forcément la notion d’erreur. D’où l’intérêt de calculer la fonction coût. En effet, pour chaque point \(x_{i}\), la fonction hypothèse associe une valeur définie par \(h(x_{i})\) qui est plus ou moins proche de \(y_{i}\). On définit ainsi « l’erreur unitaire » pour \(x_{i}\) par \((h(x_{i}) - y_{i})^{2}.\)
L’erreur unitaire pour \(x_{i}\) étant définie, on peut ensuite sommer les erreurs pour l’ensemble des points :
\[ \sum_{i=1}^{m} (h(x_{i}) - y_{i})^{2} .\]
La fonction de coût est alors définie en normant cette somme par le nombre \(m\) de points dans la base d’apprentissage :
\[ J(\theta_{0}, \theta_{1}) = \dfrac{1}{2m} \sum_{i=1}^{m} (h(x_{i}) - y_{i})^{2} .\]
En effet, la fonction de coût est obtenue en calculant la moyenne des erreurs le tout multipliée par \(\dfrac{1}{2}\). En réalité, cette fonction porte le nom de erreur quadritique moyenne (MSE) et on parle de Mean Square Error en anglais.
Entre autres, si on remplace \(h\) par son expression, on obtient finalement l’expression suivante :
\[ J(\theta_{0}, \theta_{1}) = \dfrac{1}{2m} \sum_{i=1}^{m} (\theta_{0} + \theta_{1}x_{i} - y_{i})^{2} .\]
On remarquera que \(h\) est une fonction de \(x\) et que \(J\) est par construction une fonction des paramètres \((\theta_{0}, \theta_{1})\) telle que \(h\) définit une droite affine où \(\theta_{0}\) est l’ordonnée à l’origine et \(\theta_{1}\) est la pente (ou coefficient directeur) de \(h\).
Remarque :
Dans le cadre d’une régression linéaire, le coefficient de détermination \(R^2\) peut être défini à travers d’autres fonctions d’erreur.
Il s’agit des erreurs SSE « error sum of squares » définie par :
\[ SSE = \sum_{i = 1}^n e_{i}^2 = \sum_{i = 1}^n (y_{i} - \widehat{y_{i}})^2 \]
ainsi que l’erreur SST définie comme suit :
\[ SST = \sum_{i = 1}^n (y_{i} - \overline{y_{i}})^{2}. \]
D’où finalement, le coefficient de détermination \(R^2\) n’est rien d’autre que la différence de 1 et du rapport de l’erreur SSE sur l’erreur SST :
\[ R^2 = 1- \dfrac{SSE}{SST}. \]
Minimisation de la fonction coût
Ainsi, trouver les meilleurs paramètres \((\theta_{0}, \theta_{1})\) de \(h\) et donc la meilleure droite pour modéliser notre problème équivaut exactement à trouver le minimum de la fonction coût \(J\).
Notons que la fonction coût \(J\) est telle que :
pour \(\theta_{0}\) donné, \(J\) est une fonction de \(\theta_{1}^{2}\);
pour \(\theta_{1}\) donné, \(J\) est une fonction de \(\theta_{0}^{2}\).
Pour l’une de ces deux dimensions, c’est-à-dire en fixant l’un de ces deux paramètres, la fonction \(J\) est une parabole. En tenant compte des deux dimensions, c’est-à-dire en se plaçant dans l’espace \((\theta_{0}, \theta_{1})\), \(J\) aura donc une forme convexe. L’importance de la convexité de la fonction de coût tient dans la méthode utilisée pour la minimiser.
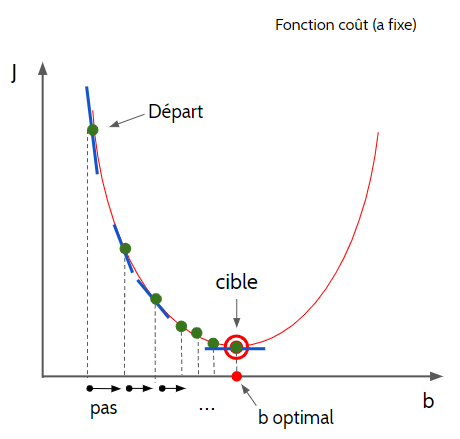
En effet, une façon de trouver le meilleur couple \((\theta_{0}, \theta_{1})\), est la descente de gradient, méthode itérative dont le principe est assez intuitif : que ferait une balle lâchée assez haut d’un bol ? Elle prendrait, à chaque instant, la meilleure pente jusqu’au point bas du bol. La formulation mathématique de cette intuition est définie comme suit :
Dans un premier temps, effectuons un changement de variable des paramètres \(\theta_{0}\) et \(\theta_{1}\) en \(\beta\) et \(\alpha\) respectivement dans le but de nous simplifier la démonstration. Pour commencer, nous allons fixer \(\beta\) et donc \(J(\alpha , \beta )\) devient une fonction de \(\alpha\) et la méthode qui sera décrite par la suite est une discrétisation.
Toutefois, en nous basant du schéma (Fig17) ci-dessous, nous allons considérer un premier réel \(\alpha_0\).
Par la suite, on calculera le gradient de \(J\) en \(\alpha_0\) c’est-à-dire \(\dfrac{\partial J(\alpha_0)}{\partial \alpha}\) puis on définira un pas noté \(\lambda\) nous permettant de passer de \(\alpha_0\) en \(\alpha_1\).
Autrement dit, à chaque itération, on choisit la meilleure « pente » sur notre fonction \(J\) pour se diriger itération après itération vers le minimum de notre fonction.
Ainsi, pour \(\alpha_0\) donné, \(\alpha_1\) est définie par :
\[\alpha_1 = \alpha_0 - \lambda \frac{\partial J(\alpha_0)}{\partial \alpha}\] puis
\[\alpha_2 = \alpha_1 - \lambda \frac{\partial J(\alpha_1)}{\partial \alpha} \] ainsi de suite etc …
Finalement, on obtient une formule itérative telle que pour tout entier \(i\) on a :
\[\alpha_{i+1} = \alpha_i - \lambda \frac{\partial J(\alpha_i)}{\partial \alpha}\] où \[ \frac{\partial J(\alpha , \beta)}{\partial \alpha} = \frac{1}{m} \sum_{i=1}^{m} x_i (\alpha x_i + \beta - y_i) .\]
Par analogie, nous allons procéder de la même sorte dans le cas où cette fois-ci c’est \(\alpha\) qui est fixé. Ainsi, \(J(\alpha , \beta )\) devient une fonction de \(\beta\).
Donc pour \(\beta_0\) donné, \(\beta_1\) est définie par :
\[ \beta_1 = \beta_0 - \lambda \frac{\partial J(\beta_0)}{\partial \beta} \] puis
\[\beta_2 = \beta_1 - \lambda \frac{\partial J(\beta_1)}{\partial \beta} \]
ainsi de suite etc …
De même, on obtient une formule itérative telle que pour tout entier \(i\) on a : \[\beta_{i+1} = \beta_i - \lambda \frac{\partial J(\beta_i)}{\partial \beta} \]
où sauf que pour le gradient par rapport à \(\beta\) on a :
\[ \frac{\partial J(\alpha , \beta)}{\partial \beta} = \frac{1}{m} \sum_{i=1}^{m}(\alpha x_i + \beta - y_i) .\]
D’où finalement après la formulation intuitive décrite ci-dessus, voici une formulation mathématique généralisante.
- itération 0 : initialisation d’un couple \((\theta_{0}, \theta_{1})\);
- itérer jusqu’à convergence :
\[\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta), \,\,j \, \in \lbrace 0, 1 \rbrace .\]
Remarque :
La vitesse de convergence dépendra notamment de l’initialisation plus ou moins heureuse de l’itération. Par ailleurs, dans le cas d’une fonction non convexe, une initialisation malheureuse peut conduire à trouver un minimum local pour \(J\). Entre autres, un couple \((\theta_{0}, \theta_{1})\) trouvé grâce un minimum local de \(J\) correspond une fonction \(h\) qui est loin d’être optimale. La convexité de \(J\) résout cet épineux problème puisque pour une fonction convexe, tout minimum local est aussi le minimum global.
Par ailleurs, on note la présence d’un facteur \(\alpha\) devant la dérivée partielle de \(J\) dans la formulation de la descente de gradient. Ce facteur \(\alpha\), qu’on appelle le «learning rate» représente physiquement la vitesse à laquelle nous souhaitons terminer nos itérations. Plus \(\alpha\) est grand, plus le pas est grand entre deux itérations, mais plus la probabilité de passer outre le minimum, voire de diverger, est grand.
À l’inverse, plus \(\alpha\) est petit et plus on a de chance de trouver le minimum, mais plus longue sera la convergence.
Avant de terminer cette partie, procédons à la formulation matricielle de la méthode de la descente du gradient résumant ainsi les différentes parties de cette section.
Formulation Matricielle de la Méthode de la Descente du Gradient :
Dans le cas d’une régression linéaire, on a une seule variable donc \(n = 1\). Et de ce fait, notre base de données sera constituée par les deux vecteurs colonnes suivants :
\[ X_0 = \left( \begin{array}{c} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(i)} \\ \vdots \\ x^{(m)} \end{array} \right) \]
et
\[ Y = \left( \begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(i)} \\ \vdots \\ y^{(m)} \end{array} \right) \]
où \(X_0\) est la variable explicative (feature) et \(Y\) la variable dépendante ou cible (target).
Ainsi, pour \(x^{(i)}\) donnée, la fonction d’hypothèse est définie par : \[ h(x^{(i)}) = \alpha x^{(i)} + \beta \] qui traduit une droite où \(\alpha\) est la pente et \(\beta\) le biais du modèle. De ce fait, après que la fonction d’hypothèse \(h(x^{(i)})\) soit bien illustrée, nous allons considérer la matrice \(H(X)\) associée au vecteur \(X\) de dimension \(m \times (n+1)\) (\(n=1\)) et qui regroupe tous les \(h(x^{(i)})\), \(i = 1, \cdots, m\).
On a
\[ H(X) = \left( \begin{array}{c} h(x^{(1)}) \\ h(x^{(2)}) \\ \vdots \\ h(x^{(i)}) \\ \vdots \\ h(x^{(m)}) \end{array} \right) = X . \theta \]
où
\[ X = \left( \begin{array}{cc} x^{(1)} & 1 \\ x^{(2)} & 1 \\ \vdots & \vdots \\ x^{(i)} & 1 \\ \vdots & \vdots \\ x^{(m)} & 1 \end{array} \right) \]
et
\[ \theta = \left( \begin{array}{c} \alpha \\ \beta \end{array} \right) \]
de dimension \((n+1) \times 1\) avec \(n=1\) dans le cas d’un modèle linéaire simple.
Ainsi, après que nous ayons fini de donner la forme matricielle du modèle, nous allons cette fois ci passer à la formulation matricielle de la fonction coût \(J\).
Forme matricielle de la Fonction Coût :
Pour rappel, la fonction coût \(J(\theta)\) est définie par : \[ J(\theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})^{2} .\]
Donc, on obtient la formulation matricielle de la fonction coût \(J\) définie comme suit :
\[ J(\theta) = \frac{1}{2m} \sum(H(X) - Y)^{2} \]
\[ J(\theta) = \frac{1}{2m} \sum(X . \theta - Y)^{2} \]
Ainsi, pour finir cette étape de formulation matricielle, nous allons donner celle du gradient.
Forme matricielle du Gradient de la Fonction Coût :
On sait que :
\[ \left\{ \begin{array}{l} \frac{\partial J(\alpha , \beta)}{\partial \alpha} = \frac{1}{m} \sum_{i=1}^{m} x^{(i)} . (\alpha x^{(i)} + \beta - y^{(i)}) \\ \\ \frac{\partial J(\alpha , \beta)}{\partial \beta} = \frac{1}{m} \sum_{i=1}^{m} 1 . (\alpha x^{(i)} + \beta - y^{(i)}) \end{array} \right.\\ \\ \\ \]
Ainsi, la formulation matricielle du gradient de la fonction coût est donnée par :
\[
\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m} X^{T} . (X . \theta - Y).
\]
Résumé des étapes pour développer un Modèle de Régression Linéaire :
En résumé, voici les étapes clés dans le développement d’un modèle linéaire.
Récolter les données \((X, y)\) avec \(X, y \in \mathbb{R}^{m\times 1}\)
Donner à la machine un modèle linéaire \(H(X) = X.\theta\)
Créer la Fonction coût \(J(\theta) = \frac{1}{2m} \sum(H(X) - y)^{2}\)
Calculer le gradient et utiliser l’algorithme de la Descente du Gradient
Répéter en boucle \(\theta\) jusqu’à ce qu’il converge vers son minimum c’est-à-dire : \[\theta := \theta - \lambda \frac{\partial}{\partial \theta}J(\theta)\]
où le gradient de \(J\) est défini par :
\[\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m} X^{T} . (X . \theta - Y)\]
3.2 La Régression Linéaire Multivariée
La régression linéaire multivariée n’est qu’une généralisation des principes évoqués dans le cas de la régression linéaire simple (univarié).
Ainsi, dans cette section il s’agira d’introduire une méthode de résolution analytique pour la recherche des meilleurs paramètres du modèle.
Le modèle Multivarié :
Comme pour le cas de la régression linéaire univariée, on recherche la meilleure fonction hypothèse qui approximera les données d’entrée. En revanche, on offre plus de variables en entrée du problème, qui constituent autant de degrés de liberté à la fonction \(h\) pour approximer au mieux les données d’entrée. Ainsi, compte tenu de ces nouvelles hypothèses, \(h\) prend une forme plus générale pour \(n\) variables d’entrée :
\[ h(x^{(i)}) = \theta_0 + \theta_1 x_{1}^{(i)} + \theta_2 x_{2}^{(i)} + \cdots + \theta_n x_{n}^{(i)} .\]
Les données d’entrée se représentent sous forme d’une matrice de dimension \(m\times (n+1)\), telle que présentée ci-dessous :
\[ X = \left( \begin{array}{ccccc} 1 & x_{1}^{(1)} & x_{2}^{(1)} & \cdots & x_{n}^{(1)}\\ 1 & x_{1}^{(2)} & x_{2}^{(2)} & \cdots & x_{n}^{(2)}\\ \vdots & \vdots & \vdots & x_{j}^{(i)} & \vdots\\ 1 & x_{1}^{(m)} & x_{2}^{(m)} & \cdots & x_{n}^{(m)} \end{array} \right) \]
\(x_{j}^{(i)}\) correspond à la valeur prise par la variable \(j\) de l’observation \(i.\)
La fonction de coût est encore une fois une simple généralisation de ce que nous avons vu précédemment. Elle est de la forme :
\[ J(\theta) = \dfrac{1}{2m} \sum_{i=1}^{m} (h(x^{(i)}) - y^{(i)})^{2} .\]
Et pour minimiser \(J\), nous pouvons utiliser la méthode générale de la descente de gradient que nous rappelons :
- itération 0 : initialisation d’un vecteur \((\theta_0, \theta_1, \theta_2, \cdots , \theta_n)\)
- itérer jusqu’à convergence :
\[\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta), \,\,j \, = 0, 1, \cdots ,n.\]
\(J\) étant toujours convexe, nous n’aurons pas de problème de minima locaux. En revanche, et c’est la nouveauté de cette section, nous risquons de rencontrer un problème avec cette méthode de résolution si nos variables évoluent avec des échelles très différentes. Ainsi, pour pallier à ce problème nous faisons recours à la standardisation de nos données.
En effet, standardiser les données consiste à utiliser la fonction suivante : \[ X_{std} = \dfrac{X - \min(X)}{\max(X) - \min(X)} \] La fonction ci-dessus normalise les variables de sorte qu’elles évoluent entre 0 et 1.
En supposant que nos données soient standardiser (données de même échelle), la descente de gradient peut être appliquée à la régression linéaire multivariée.
4. Application : Prédiction du Coût d’Assurance Maladie
Dans cet article, nous utilisons le langage de programmation, de traitement des données et d’analyse statistique R.

Et pour l’implémentation des algorithmes de « Machine Learning » sur R, nous faisons recours à l’une des librairies principales dédiée en ce sens. Il s’agit de la librairie tidymodels.
Tidymodels est un framework, une collection de packages pour la modélisation et l’apprentissage automatique utilisant les principes tidyverse.
Elle couvre une large fraction de la pratique de l’analyse prédictive (classification et régression). Un peu à la manière de “scikit-learn” pour Python. Elle intègre dans un ensemble cohérent les étapes clés de la modélisation :
- découpage des données (train/test),
- prétraitement des données,
- apprentissage des modèles,
- évaluation des modèles et
- déploiement des modèles.
La standardisation des prototypes des fonctions d’apprentissage et de prédiction notamment permet de simplifier notre code, facilitant les tâches d’optimisation et de comparaison des modèles.
Dans cette section, à partir d’un exemple de régression “prédiction des chrages d’assurance”, nous montrons quelques facettes du package “tidymodels”.
Données
Pour rappel, nous traitons les données « Medical Insurance dataset » lien du dataset. Il s’agit de prédire le coût de la couverture d’assurance maladie. Nous disposons près de 1338 observations et 7 variables prédictives (qualitatives et quantitatives).
Subdivision apprentissage-test
Même si “tidymodels” propose des techniques de rééchantillonnage pour l’évaluation des modèles, nous allons subdiviser les données en échantillons d’apprentissage (80%) et de test (20%). Nous utilisons la commande « initial_split() » de la librairie “tidymodels”. Elle produit un index des individus à inclure dans l’ensemble d’apprentissage.
Elaboration des Modèles de Machine Learning
Dans le cadre de cette étude, nous en avons ciblé 5 « Modèles de Machine Learning » auxquels nous décidons d’entrainer sur nos données. Il s’agit principalement des modèles :
- glmnet : Lasso and Elastic-Net Regularized Generalized Linear Models
- rf : Random Forest
- XGBoost : eXtreme Gradient Boosting
- CUBIST Model
- EARTH Model
Exemple : cas du modèle GLMNET
Ainsi, après entrainement des modèles, nous avons procédé à leur évaluation sur le Jeu de Test. Et pour cela, nous baserons des métriques RMSE (Erreur Quadritique Moyenne) définie par :
\[ RMSE = \sqrt{\dfrac{1}{2m} \sum_{i=1}^{m} (\widehat{y_{i}} - y_{i})^{2}} \]
ainsi que le coefficient de détermination \(R^2\).
Classement des Modèles de Machine Learning sur le jeu de test
Le tableau ci-dessous, nous donne un classement des 5 modèles qui ont été entrainés sur nos données. Le classement se fait selon les métriques RMSE et \(R^2\).
De ce fait, les données montrent que le modèle Random Forest est le plus performant sur notre jeu de test (avec la plus petite erreur, RMSE = 0.15). Toutefois, on se demande si ce dernier n’est pas surajusté. Pour cela, il est important de comparer les performances du modèle sur le jeu de test ainsi que celui d’entraînement. On parle souvent du phénomène « overfitting » des modèles.
Tab4 : Tableau de classement des Modèle de ML
Surajustement ou « Overfitting » des Modèles :
Le surajustement est un comportement indésirable d’apprentissage automatique qui se produit lorsque le modèle d’apprentissage automatique fournit des prédictions précises pour les données d’entraînement mais pas pour les nouvelles données (test).
En effet, lorsque les data scientists utilisent des modèles d’apprentissage automatique pour établir des prévisions, ils entraînent d’abord le modèle sur un ensemble de données connu (données d’entraînement). Ensuite, sur la base de ces informations, le modèle tente de prédire les résultats pour de nouveaux ensembles de données (données de test). Un modèle de surajustement peut donner des prévisions inexactes et ne pas être performant pour tous les types de nouvelles données.
Pour ce qui est de notre étude, les données montrent que sur l’ensemble des modèles entraînés, les résultats sont meilleurs sur le jeu de test que sur le jeu d’entraînement. Donc, nos modèles n’ont pas overffité (pas de surajustement) comme on peut le voir à travers la figure Fig18 ci-dessous.
Entre autres, considérons le coefficient de détermination \(R^2\) qui est un indicateur qui permet de juger la qualité d’une régression linéaire. Il mesure l’adéquation entre le modèle et les données observées ou encore à quel point l’équation de régression est adaptée pour décrire la distribution des points.
De ce fait, avec \(R^2 = 0.86\), cela signifie que l’équation de la droite de régression est capable de déterminer 86% de la distribution des points.
D’où finalement, nous pouvons considérer le modèle Random Forest comme étant celui le plus performant sur nos nos données.
Remarque :
L’une des meilleures manières d’améliorer la performance des modèles de Machine Learning, c’est de faire recourir aux hyperparamètres.
Ils contrôlent directement la structure, la fonction et la performance du modèle. Le réglage des hyperparamètres permet aux spécialistes des données (data scientist) d’ajuster les performances du modèle pour obtenir des résultats optimaux. Ce processus est une partie essentielle du machine learning, et le choix des valeurs appropriées des hyperparamètres est crucial pour le succès.
Ainsi, la figure ci-dessous (Fig19) traduit la distribution des hyperparamètres pour ce qui est du modèle Random Forest. Autrement, elle illustre les meilleurs de ces derniers ayant conduit au modèle le plus performant.
Comparaison entre Valeurs Réelles (Actual) & Prédictions (Predicted) :
Après plusieurs étapes de validation des modèles, nous voilà enfin arrivés à l’étape finale concernant la confrontation de nos prédictions avec les valeurs réelles (coût d’assurance) des données.
A priori, les données montrent une évolution linéaire de pratiquement tous les nuages de points au tour de la droite de régression. Ceci traduit la précision et la bonne qualité des prédictions du modèle Random Forest.
5. Analyse des Facteurs sur le Coût de la Couverture d’Assurance Maladie
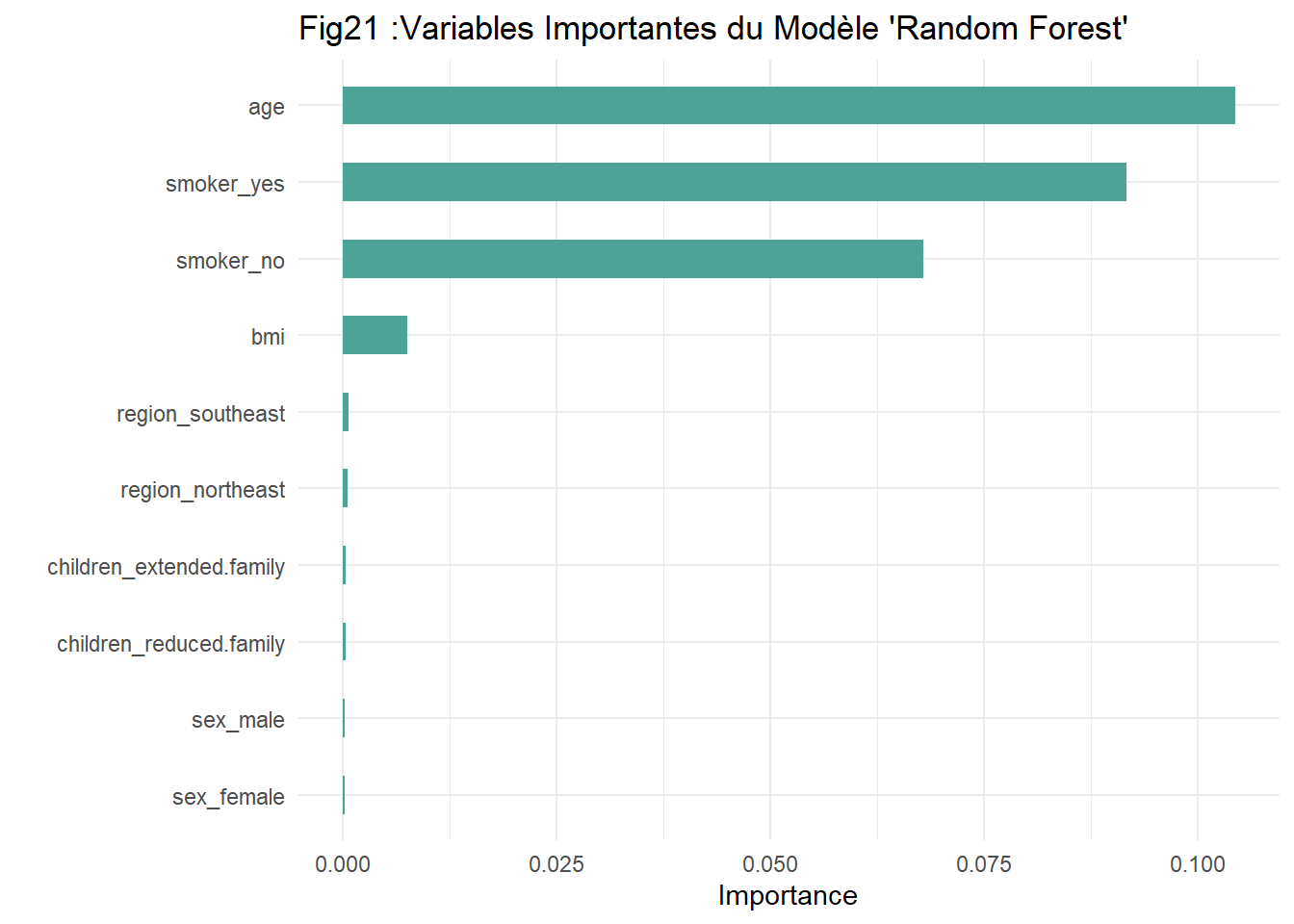
Sur R, la fonction « vip » de la librairie VIP nous fournit les 10 variables les plus influentes de notre modèle autrement dit, celles qui sont susceptibles d’expliquer la variabilité du coût d’assurance maladie.
Ainsi, d’après la figure ci-dessous (Fig21), on note que l’âge principalement, le fait de fumer ou pas (smoker) et l’indice de masse corporelle (bmi) sont dans cet ordre les variables qui influenceraient le plus sur la prédiction des coûts ou charges de couverture d’assurance maladie.
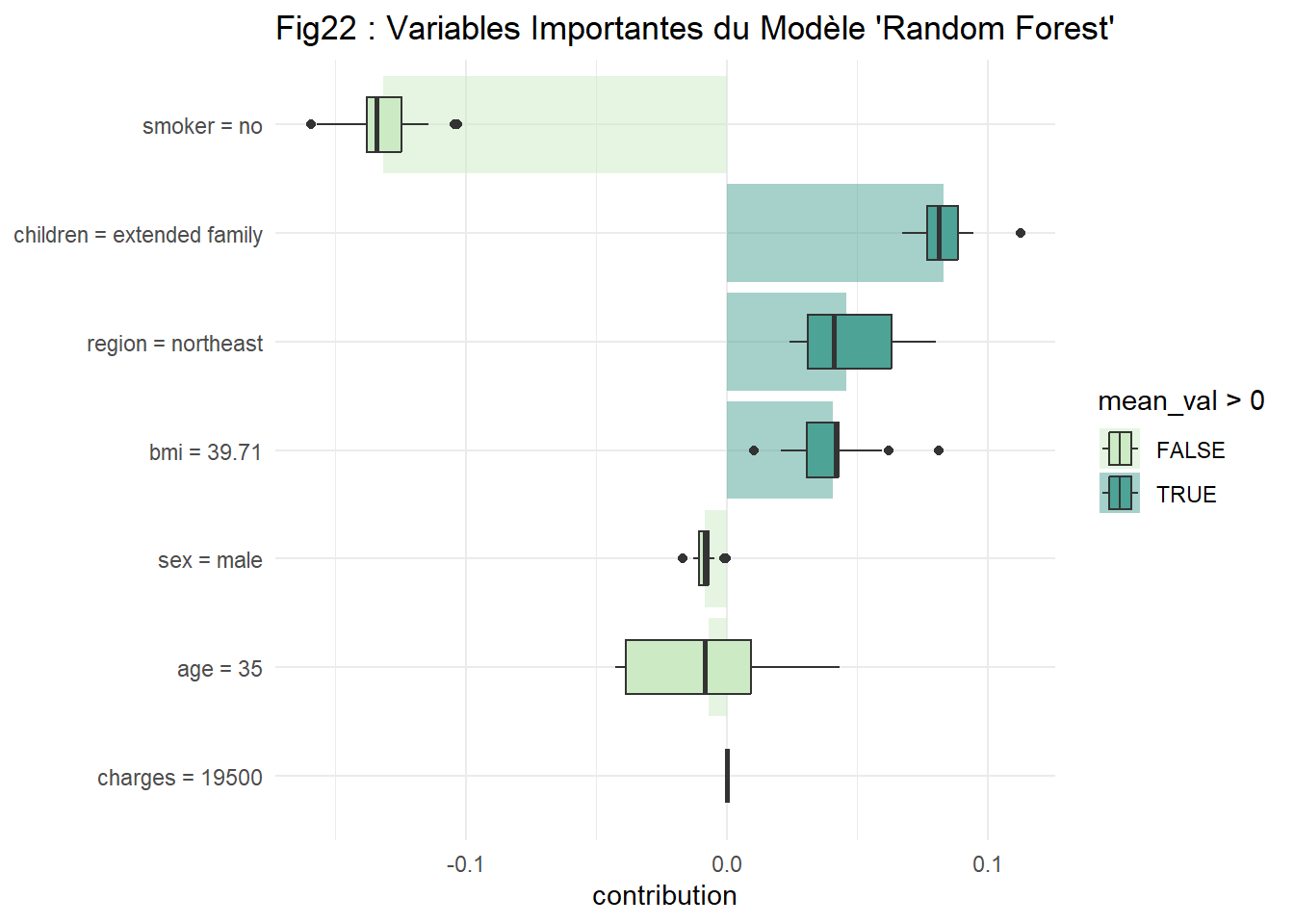
Explication du Modèle Random Forest via la librairie « DALEXtra »
La librairie « DALEXtra » nous fournit une palette de fonctions nous permettant d’expliquer les modèles de Machine Learning. En effet, elle nous permet d’expliquer la variabilité du modèle dans la prédiction du coût d’assurance maladie.
A travers la figure ci-dessus (Fig22), on voit que le fait d’appartenir à une famille large (extended family), le fait de résider dans la zone nord-est et le fait d’avoir un indice de masse corporelle (bmi) égale à 40, tous ces facteurs ont un impact positif sur la prédiction des coûts d’assurance maladie. Autrement dit, les individus qui prennent ces valeurs se verront augmenter de leur coût d’assurance maladie.
Alors que par ailleurs, on voit que les non-fumeurs, les hommes en particulier ainsi que les âgés de 35 ans se voient par contre, diminuer de leur coût d’assurance maladie.
6. Conclusion
Le profit est le but recherché de toute entreprise. En ce sens, il est impératif de trouver une bonne stratégie de marketing pour optimiser les gains. L’étude a montré que selon que l’on prenne certaines caractéristiques (âge, sexe, type de famille ou fumeur) le coût peut être élevé ou moindre. Ainsi, le profilage de la clientèle demeure une bonne option pour assigner la meilleure formule à chaque type de client. Par exemple, l’étude a montré que les personnes âgées ainsi les fumeurs sont les plus facturés par rapport aux autres. Toutefois, il est important de prendre en compte tous facteurs sous-jacents cachés dans nos données.
Et donc, pour résoudre la problématique, imaginez si nous disposions d’un dispositif prédictif intelligent qui, une fois qu’il ait fini de recevoir en entrée les caractéristiques observables d’un client, serait capable de nous prédire le coût adéquate pour une couverture d’assurance maladie.
Alors, découvrez « HICP APP » le dispositif intelligent de prédiction du coût de la couverture d’assurance maladie développé en ce sens. 👇👇(Cliquez dessus)
En effet, il s’agit d’une application qui a été développée avec via la librairie Shiny de R. Elle facilite la création d’applications Web interactives directement à partir de R.
🤩 Vous pouvez nous suivre sur YouTube sur la Chaîne SN4AI👇
👉 Merçi de vous Abonnez, de Liker et de Partager !
😍 Vous trouverez sur SN4AI plusieurs thématiques à savoir :
Création de Cartographie sur R avec les données de la Covid-19 (analyse et traitement des données) 👉 Cartographie avec R
Initiation à l’intelligence artificielle 👉 ici
L’attrition des clients (Churn) : Prédiction du risque de désabonnement par Apprentissage Automatique (Machine Learning) 👉 Prédiction du risque de désabonnement
Visualisation des données avec R (analyse et traitement des données) 👉 ici
Projets developpés sur AI Accuracy Consulting 👉 ici
🤗Merçi de vous Abonnez, de Liker et de Partager !